Breusch–Pagan Test for Heteroscedasticity

At a high-level, various tests for heteroscedasticity in ordinary least squares (OLS) follow the same basic logic. The main idea is that the scedasticity of the OLS residuals will resemble the scedasticity of the true errors. This is because the OLS estimator is consistent ($\hat{\boldsymbol{\beta}}$ converges in probability to $\boldsymbol{\beta}$) regardless of scedasticity. Put differently, the proof that $\hat{\boldsymbol{\beta}}$ is consistent does not depend on the standard homoscedasticity assumption. Thus, any heteroscedasticity in the true error terms should be detectable in the residuals, which estimate the errors. These tests, then, are ultimately hypothesis tests applied to the OLS residuals (Greene, 2003).

The goal of this post is to understand a simple test for heteroscedasticity, the Breusch–Pagan test, which exemplifies this process. I’ll first discuss the main idea and then demonstrate the test on a toy problem.

Main idea

The basic idea of the Breusch–Pagan test is as follows. Suppose we run a linear regression,

$y_n = \beta_0 + \boldsymbol{\beta}^{\top} \mathbf{x}_n + \varepsilon_n, \tag{1}$

where we assume that each $\varepsilon_n$ is identically and normally distributed with mean zero and variance one. Now let’s express the variance of each datum as a function of some function $f(\cdot)$, which does not depend on $n$:

$\sigma_n^2 = f(\alpha_0 + \boldsymbol{\alpha}^{\top} \mathbf{x}_n). \tag{2}$

Here, $\boldsymbol{\alpha} = \begin{bmatrix} \alpha_1 & \dots & \alpha_P \end{bmatrix}^{\top}$ is a $P$-vector of coefficients which are independent of the coefficients $\boldsymbol{\beta}$. Why are we doing this? We’d like to test for heteroscedasticity. We can say that the null hypothesis is that the model has homoscedasticity, and this would require that

$\textsf{H}_0 : \alpha_1 = \alpha_2 = \dots = \alpha_P = 0. \tag{3}$

In other words, if we have homoscedasticity, than the conditional variance of each error term would not depend on $n$ or $\mathbf{x}_n$, i.e.

$\mathbb{V}[\varepsilon_n \mid \mathbf{X}] = \sigma_n^2 = f(\alpha_0). \tag{4}$

The null hypothesis (Equation $3$) implies that $\sigma_n^2$ is a constant.

So performing the Breusch–Pagan test amounts to the following: fit the linear model in Equation $1$; estimate the error terms’ variances using the squared residuals; run a second regression to estimate $\boldsymbol{\alpha}$ in Equation $2$; and finally check if $\boldsymbol{\alpha}$ is “close enough” to $\mathbf{0}$.

In detail

To make “close enough” a precise claim, we should perform a hypothesis test. To do that, we need to prove that some statistic of the regression implied by Equation $2$ has a well-behaved distribution, such that we can compute $p$-values. Proving this is the main result in (Breusch & Pagan, 1979).

To state Breusch and Pagan’s result, let $e_n$ denote the $n$-th residual, the OLS estimate of $\varepsilon_n$. Now define the estimated residual variance as

$\hat{\sigma}_{\varepsilon}^2 = \frac{1}{N} \sum_{n=1}^N e_n^2. \tag{5}$

This is just the residual sum of squares since $e_n$ has mean zero. Now define $g_n$ as

$g_n = \frac{e_n^2}{\hat{\sigma}_{\varepsilon}^2}. \tag{6}$

In words, $g_n$ is the proportion of the residual variance that is explained by the $n$-th sample. Now fit a linear regression with the original data $\mathbf{X}$ as the predictors and $\mathbf{g} = \begin{bmatrix} g_1 & \dots & g_N \end{bmatrix}^{\top}$ as the response:

$g_n = \alpha_0 + \boldsymbol{\alpha}^{\top} \mathbf{x}_n + u_n. \tag{7}$

Finally, compute the explained sum of squares from this second regression. Breusch and Pagan showed that, when the null hypothesis is true, one-half of this explained sum of squares is asymptotically distributed as $\chi^2$ with $(P-1)$ degrees of freedom.

Given that the response variables $\mathbf{g}$ should be mean centered, the explained sum of squares is just

$\sum_{n=1}^N g_n \hat{g}_n = \mathbf{g}^{\top} \hat{\mathbf{g}}, \tag{8}$

where $\hat{\mathbf{g}} = \mathbf{X} \hat{\boldsymbol{\alpha}}$. This means we can compute the desired quantity as

$\text{LM} = \frac{1}{2} \left[ \mathbf{g}^{\top} \mathbf{X} (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{g} \right]. \tag{9}$

since $\hat{\boldsymbol{\alpha}} = (\mathbf{X}^{\top} \mathbf{X})^{-1} \mathbf{X}^{\top} \mathbf{g}$. This is traditionally denoted “LM” because the Breusch–Pagan test is a Lagrange multiplier test or score test.

To summarize, we simply run both regressions, compute $\text{LM}$ in Equation $9$, and then test the null hypothesis,

$\textsf{H}_0 : \text{LM} \sim \chi_{P-1}^2. \tag{10}$

We can then accept or reject the null hypothesis for our specific confidence level.

Example and implementation

In a previous post on OLS with heteroscedasticity, I gave a simple example of data on which OLS estimated incorrect $t$-statistics.

from   numpy.random import RandomState
import statsmodels.api as sm

rng   = RandomState(seed=0)
x     = rng.randn(1000)
beta  = 0.01
noise = rng.randn(1000) + x*rng.randn(1000)
y     = beta * x + noise

ols = sm.OLS(y, x).fit()
print(f'{ols.params[0]:.4f}')   # beta  : -0.1634
print(f'{ols.tvalues[0]:.4f}')  # t-stat: -3.7863

Let’s revisited this example, and see if the Breusch–Pagan test can detect heteroscedasticity in advance. Here is a simple Python implementation of the test (for univariate data), fit using the OLS result and predictors in the example above:

from scipy.stats import chi2

def breusch_pagan(resid, x):
    g     = resid**2 / np.mean(resid**2)
    ols   = sm.OLS(g, sm.add_constant(x)).fit()
    beta  = ols.params[1]
    g_hat = x * beta
    lm    = 0.5 * g.T @ g_hat
    pval  = chi2(1).pdf(lm)
    return lm, pval

lm, pval = breusch_pagan(ols.resid, x)
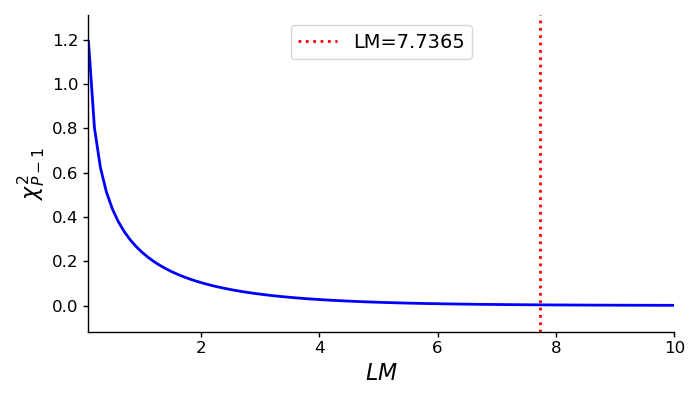
print(f'{lm:.4f}')                    # 7.7365
print(f'{pval:.4f}')                  # 0.0030
print(f'Reject null? {pval < 0.05}')  # True

We can see that the Breusch–Pagan test rejects the null hypothesis of homoscedasticity using a $95\%$ confidence level (Figure $1$).

Figure 1. The $\chi^2_{P-1}$ distribution ($P = 1)$, along with the value of the Breusch–Pagan test statistic (Equation $9$) for the example data (red dashed line). Since this test result is unlikely ($p$-value of $3\%$), we reject the null hypothesis of homoscedasticity.