Convex Combinations as Lines

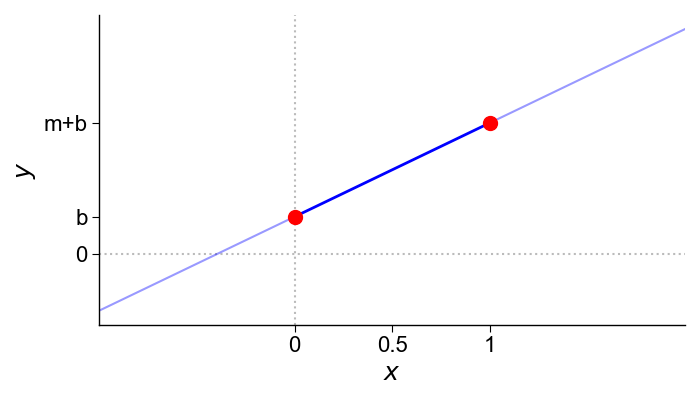
The locus of all convex combinations of two points is the line between them. This is easy to visualize in two dimensions. Consider the linear equation

$y(x) = mx + b \tag{1}$

where $m$ is the slope of the line and $b$ is the bias or $y$-intercept. We can rewrite this as

$\begin{aligned} y(x) &= mx + b \\ &= x [m + b - b] + b \\ &= x (m + b) + (1 - x) b. \end{aligned} \tag{2}$

This equation is a linear combination of two points, $(0, b)$ and $(1, m+b)$. When $0 \leq x \leq 1$, the equation is a convex combination of the two points and defines a line between them. When $x \leq 0$, the equation traces a line to the left of $(0, b)$. When $x \geq 1$, the equation traces a line to the right of $(1, m+b)$ (Figure $1$).

Figure 1. The line $y(x) = x (m + b) + (1 - x) b$ is a linear combination of the points $(0, b)$ and $(1, m+b)$.

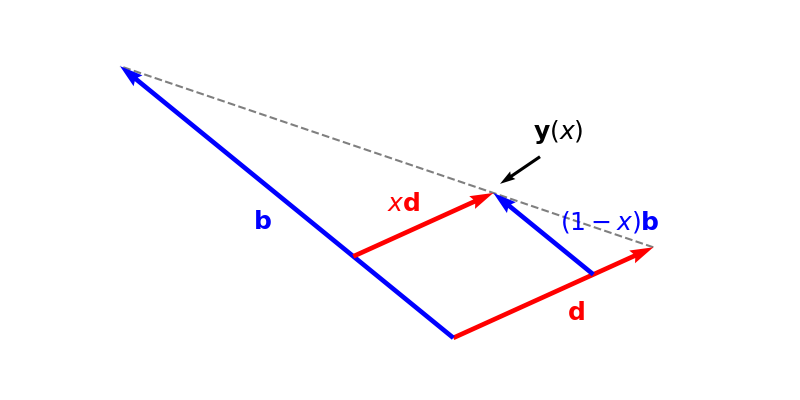
We can extend this visualization to arbitrary dimensions. Consider a vector $\mathbf{y}(x)$ that is the convex combination of two vectors $\mathbf{d}$ and $\mathbf{b}$:

$\mathbf{y}(x) = x \mathbf{d} + (1-x) \mathbf{b}, \qquad 0 \leq x \leq 0. \tag{3}$

We could visualize this as vector addition. As $x$ varies between zero and one, the two vectors $x \mathbf{d}$ and $(1-x) \mathbf{b}$ add to produce a new vector $\mathbf{y}(x)$ (Figure $2$).

Figure 2. The line $\mathbf{y}(x)$ defined as a convex combination of $\mathbf{b}$ and $\mathbf{d}$.

Another way to visualize this is to use Equation $1$. Let’s rewrite Equation $3$ as

$\begin{aligned} \mathbf{y}(x) &= x \mathbf{d} + (1-x) \mathbf{b} \\ &= x \mathbf{d} + (1-x) \mathbf{b} + x \mathbf{b} - x \mathbf{b} \\ &= x (\mathbf{d} - \mathbf{b}) + \mathbf{b}. \end{aligned} \tag{4}$

(Clearly, a vector $\mathbf{m}$ could be defined as $\mathbf{m} \triangleq \mathbf{d} - \mathbf{b}$.) Now we can think of $\mathbf{y}(x)$ as simply a fraction of the vector subtraction $\mathbf{d} - \mathbf{b}$ plus $\mathbf{b}$ (Figure $3$). While Figure $3$ is not a proof, I think it provides useful intuition: as $x$ ranges between zero and one, the vector $x (\mathbf{d} - \mathbf{b})$ ranges between the two end points defined by $\mathbf{b}$ and $\mathbf{d}$. The vector $\mathbf{y}(x)$ is just this fractional distance plus $\mathbf{b}$.

Figure 3. The line $\mathbf{y}(x)$ defined as $\mathbf{b}$ plus $\mathbf{d} - \mathbf{b}$ rescaled by $x$.

Now that we some geometric intuition, let’s prove that $\mathbf{y}(x)$ must be on the line between $\mathbf{b}$ and $\mathbf{d}$. First, let’s compute the distance between $\mathbf{b}$ and $\mathbf{y}(x)$:

$\begin{aligned} \lVert \mathbf{b} - \mathbf{y}(x) \rVert &= \lVert \mathbf{b} - [x (\mathbf{d} - \mathbf{b}) + \mathbf{b}] \rVert && \text{(Equation $4$)} \\ &= \lVert - x (\mathbf{d} - \mathbf{b}) \rVert \\ &= | x | \lVert (\mathbf{b} - \mathbf{d}) \rVert \\ &= x \lVert \mathbf{b} - \mathbf{d} \rVert. && \text{($x \geq 0$)} \end{aligned} \tag{5}$

Next, let’s compute the distance between $\mathbf{y}(x)$ and $\mathbf{d}$:

$\begin{aligned} \lVert \mathbf{y}(x) - \mathbf{d} \rVert &= \lVert x \mathbf{d} + (1-x) \mathbf{b} - \mathbf{d} \rVert && \text{(Equation $3$)} \\ &= \lVert (x - 1) \mathbf{d} + (1-x) \mathbf{b} \rVert \\ &= \lVert (1-x) \mathbf{b} - (1 - x) \mathbf{d} \rVert \\ &= |1 - x| \lVert \mathbf{b} - \mathbf{d} \rVert \\ &= (1 - x) \lVert \mathbf{b} - \mathbf{d} \rVert. && \text{($1 - x \geq 0$)} \end{aligned} \tag{6}$

Taken together, Equations $5$ and $6$ imply that the total distance is

$\begin{aligned} \lVert \mathbf{b} - \mathbf{y}(x) \rVert + \lVert \mathbf{y}(x) - \mathbf{d} \rVert &= x \cdot \lVert \mathbf{b} - \mathbf{d} \rVert + (1 - x) \cdot \lVert \mathbf{b} - \mathbf{d} \rVert \\ &= \Vert \mathbf{b} - \mathbf{d} \rVert. \end{aligned} \tag{7}$

Thus, $\mathbf{y}(x)$ must be on the line between $\mathbf{b}$ and $\mathbf{d}$. Why? Imagine a triangle with vertices defined by $\mathbf{b}$, $\mathbf{y}(x)$, and $\mathbf{d}$ (Figure $4$).

Figure 4. A triangle with vertices $\mathbf{b}$, $\mathbf{y}(x)$, and $\mathbf{d}$. By the triangle inequality, if the sum of the lengths of any two sides is equal to the length of the remaining side, the vertices must be collinear.

Then the lengths of the sides would be

$\lVert \mathbf{b} - \mathbf{y}(x) \rVert, \qquad \lVert \mathbf{y}(x) - \mathbf{d} \rVert, \qquad \Vert \mathbf{b} - \mathbf{d} \rVert. \tag{8}$

By the triangle inequality, the sum of the first two lengths can only equal the sum of the third if we have a degenerate triangle, i.e. the triangle’s vertices are collinear. So the three vertices $\mathbf{b}$, $\mathbf{y}(x)$, and $\mathbf{d}$ must be collinear. Since we can easily verify that $\mathbf{y}(0) = \mathbf{b}$ and $\mathbf{y}(1) = \mathbf{d}$, then the locus of points defined by $\mathbf{y}(x)$ is the line between $\mathbf{b}$ and $\mathbf{d}$.