Why Backprop Goes Backward

The usual explanation of backpropagation (Rumelhart et al., 1986), the algorithm used to train neural networks, is that it is propagating errors for each node backwards. But when I first learned about the algorithm, I had a question that I could not find answered directly: why does it have to go backwards? A neural network is just a composite function, and we know how to compute the derivatives of composite functions using the chain rule. Why don’t we just compute the gradient in a forward pass? I found that answering this question strengthened my understanding of backprop.

I will assume the reader broadly understands neural networks and gradient descent and even has some familiarity with backprop. I’ll first setup backprop with some useful concepts and notation and then explain why a forward propagation algorithm is supoptimal.

Setup

Recall that the goal of backprop is to efficiently compute $\partial f / \partial \theta_i$ for every weight $\theta_i$ in a neural network $f$. To frame the problem, let’s reason about an arbitrary weight $\theta_1$ and node $v$ somewhere in $f$:

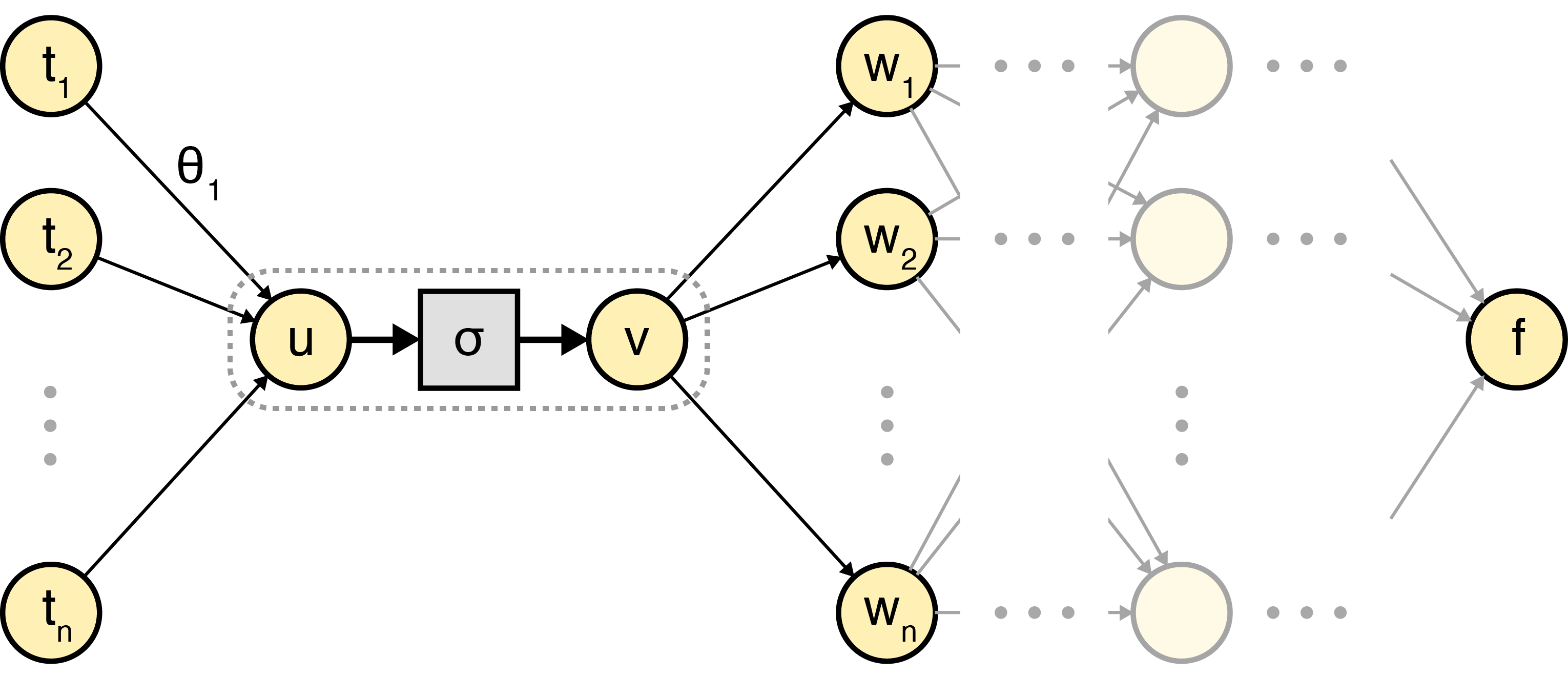
To be clear, the node $v$ refers to the output value of the node after passing the weighted sum of its inputs through an activation function $\sigma$, i.e.:

$\begin{aligned} u &= \theta_1 t_1 + \theta_2 t_2 + \dots + \theta_n t_n \\ v &= \sigma(u) \end{aligned}$

Note that in a typical diagram, $u$, $\sigma$, and $v$ would all be a single node, denoted by the dashed line. In my mind, the most important observation needed to understand backprop is this: most of computing $\partial f / \partial \theta_1$ can be done locally at every node because of the chain rule:

$\frac{\partial f}{\partial \theta_1} = \frac{\partial f}{\partial v} \frac{\partial v}{\partial u} \frac{\partial u}{\partial \theta_1}$

We can compute $\partial v / \partial u$ analytically; it just depends on the definition of $\sigma$. And we know that $\partial u / \partial \theta_1 = t_1$. So at every node $v$, if we knew $\partial f / \partial v$, we could compute $\partial f / \partial \theta_1$.

The challenge with computing $\partial f / \partial v$ is that downstream nodes depend on the value of $v$. Thankfully, the multivariable chain rule has the answer. Given a multivariable function $g(w_1, w_2, \dots, w_m)$ in which each $w_i$ is a single variable function $w_i(v)$, the multivariable chain rule says:

$\frac{\partial g}{\partial v} = \frac{\partial}{\partial v} g(w_1(v), w_2(v), \dots, w_m(v)) = \sum_{j} \frac{\partial g}{\partial w_j} \frac{\partial w_j}{\partial v}$

So we can compute $\partial f / \partial \theta_i$ for any weight $\theta_i$, meaning we have the necessary machinery to attempt to implement backprop in a forward rather than backward pass. Let’s see what happens.

Repeated terms

We want a forward propagating algorithm that can compute the partial derivative $\partial f / \partial \theta_i$ for an arbitrary weight $\theta_i$. We showed above that at node $v$, this is equivalent to:

$\frac{\partial f}{\partial \theta_i} = \frac{\partial f}{\partial v} \frac{\partial v}{\partial \theta_i}$

Note that I’ve dropped the intermediate variable $u$ for ease of notation. To design our forward propagating algorithm, let’s formalize an important fact: in a directed computational graph in which node $b$ depends upon node $a$, it is impossible to compute $\partial b / \partial a$ at any point before node $b$:

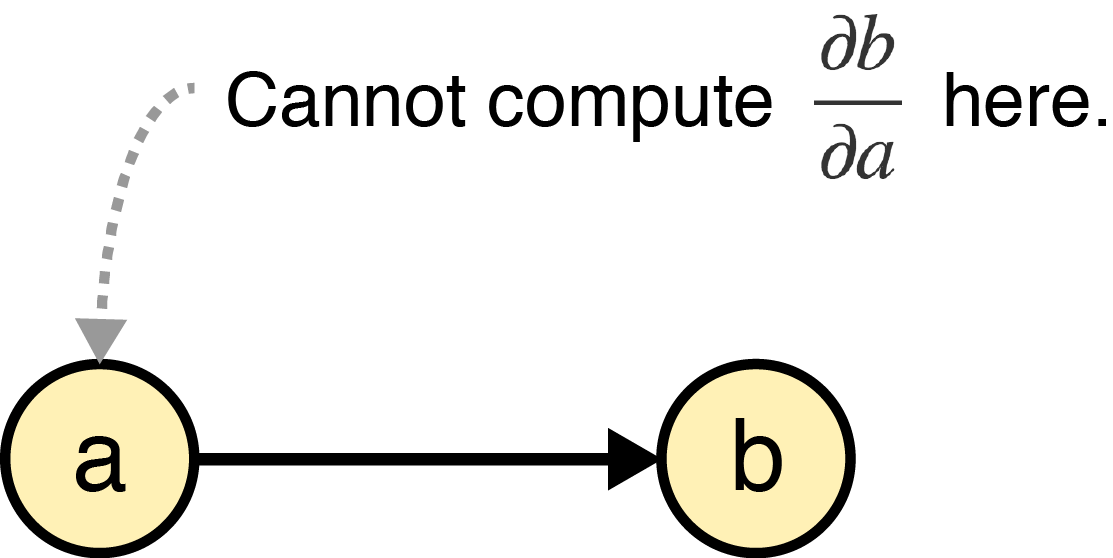
This claim should be obvious. If our computational graph represents a function $f(a) = b$, it is impossible to compute $f^{\prime}(a)$ without access to $f$ and therefore $b$.

In our setup, for every downstream node $w_j$ that depends on a node $v$, it is impossible to compute $\partial w_j / \partial v$ at node $v$. Therefore, in order to compute $\partial f / \partial v$, we must decompose the term using the multivariable chain rule and pass the other terms needed to compute $\partial f / \partial \theta_i$ forward to each node $w_j$ that depends on $v$:

$\frac{\partial f}{\partial \theta_i} = \Big( \sum_{j} \frac{\partial f}{\partial w_j} \underbrace{\frac{\partial w_j}{\partial v}}_{\text{Compute on $w_j$}} \Big) \overbrace{\frac{\partial v}{\partial \theta_i}}^{\text{Pass forward}}$

We can see that such an algorithm blows up computationally because we’re forward propagating the same message many times over. For example, if we want to compute $\partial f / \partial \theta_i$ and $\partial f / \partial \theta_k$ where $\theta_i$ and $\theta_k$ are different weights in the same layer, we need to compute $\partial v / \partial \theta_i$ and $\partial v / \partial \theta_k$ separately, but all the other terms are repeated:

$\begin{aligned} \frac{\partial f}{\partial \theta_i} = \overbrace{ \Big( \sum_{j} \Big( \sum_{k} \frac{\partial f}{\partial z_k} \frac{\partial z_k}{\partial w_j} \Big) \frac{\partial w_j}{\partial v} \Big)}^{\text{Repeated terms}} \color{#11accd}{ \frac{\partial v}{\partial \theta_i} } \\ \frac{\partial f}{\partial \theta_k} = \Big( \sum_{j} \Big( \sum_{k} \frac{\partial f}{\partial z_k} \frac{\partial z_k}{\partial w_j} \Big) \frac{\partial w_j}{\partial v} \Big) \color{#bc2612}{ \frac{\partial v}{\partial \theta_k} } \end{aligned}$

Here is a diagram of message passing the repeated terms:

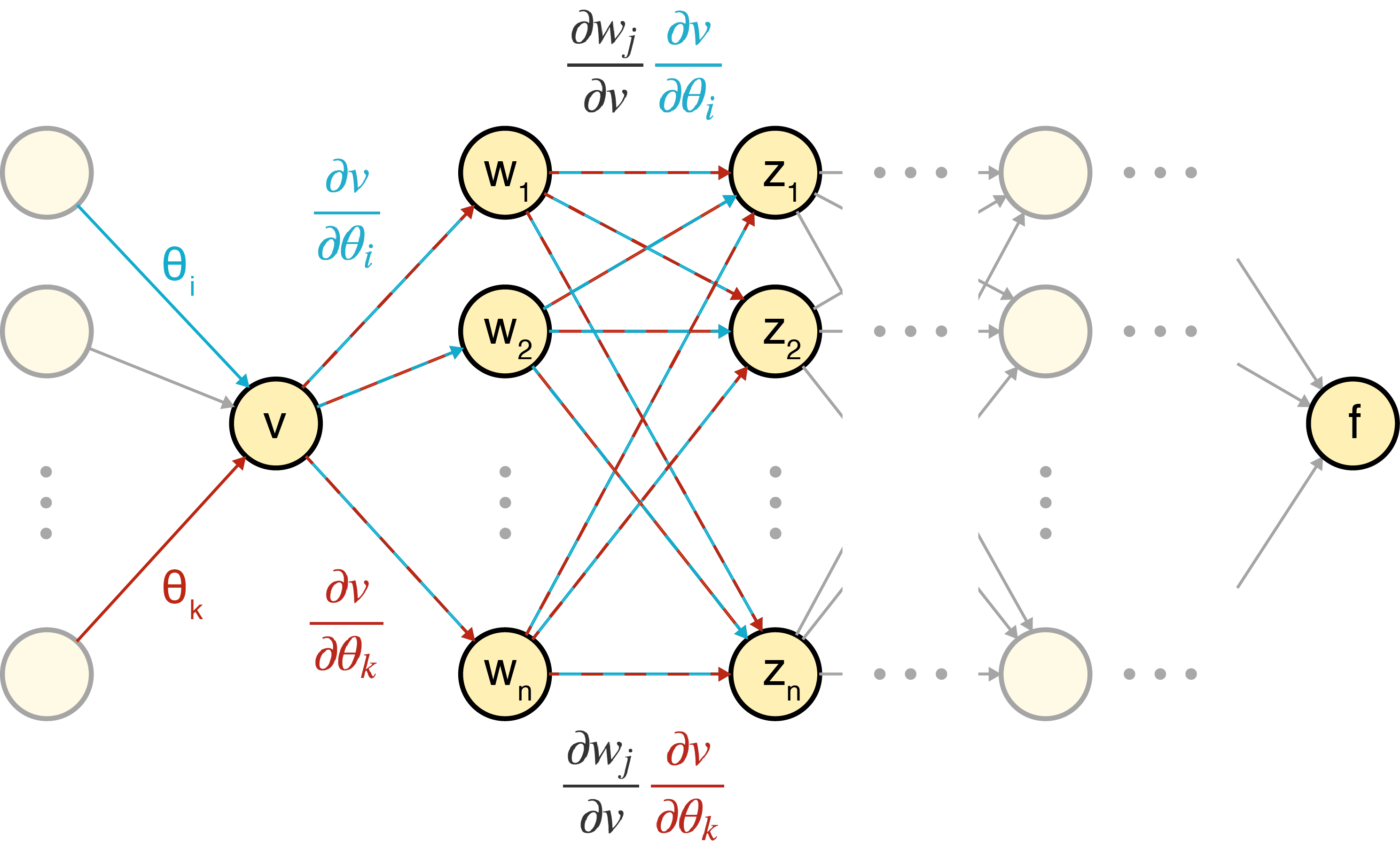
I think the above diagram is the lynchpin in understanding why backprop goes backwards. This is the key insight: if we already had access to downstream terms, for example $\partial w_j / \partial v$, then we could message pass those terms backwards to node $v$ in order to compute $\partial f / \partial v$. Since each node is just passing its own local term, the backward pass could be done in linear time with respect to the number of nodes.

A backward pass

I hope this explanation it clarifies how you might get to backprop from first principles trying to compute derivatives in a directed acyclic graph. On a given node $b$ that depends on a node $a$, we simply message pass $\partial b / \partial a$ back to $a$. The multivariable chain rule helps prove the correctness of backprop. For any node $v$ with downstream weights $w_j$, if $v$ simply sums the backwardly propagating messages, it computes its desired derivative:

$\frac{\partial f}{\partial v} = \sum_{j} \frac{\partial f}{\partial w_j} \frac{\partial w_j}{\partial v}$

Once you understand the main computational problem backprop solves, I think the standard explanation of backpropagating errors makes much more sense. This process is can be viewed as a solution to a kind of credit assignment problem: each node tells its upstream neighbors what they did wrong. But the reason the algorithm works this way is because a naive, forward propagating solution would have quadratic runtime in the number of nodes.